Numa análise exploratória de dados é muito comum que não somente os pesquisadores, mas qualquer profissional que esteja analisando dados, precise valer-se do uso do BOXPLOT. Não é nada comum fazer-se confusão com a interpretação do que o boxplot tem a fornecer como informação. Ele pode ser utilizado para visualizar a distribuição dos dados de uma variável e também para fazer-se uma comparação entre elementos da amostra e/ou variáveis.
Este post mostrará de forma resumida, através do uso de Python como fazer o boxplot e também faremos sua interpretação através de exemplos práticos.

Para a interpretação do boxplot, primeiramente, é interessante para o pesquisador, entender o conceito e diferença entre quartil e percentil.
O percentil é utilizado como uma medida de posição, onde em uma amostra ordenada e dividida em 100 partes indica onde determinado percentual de elementos encontram-se em relação ao percentual determinado. Assim, o percentil é referido como um número inteiro, entre 1 e 100, normalmente, utiliza-se os números 25, 50 e 75 que servem para dividir o espaço em quatro partes. Por exemplo, o percentil 25 refere-se ao valor da amostra que indica que 25% dos valores estão abaixo ou são iguais a ele.
A relação é Percentil25 = Percentil * Tamanho da Amostra / 100
Assim, para uma amostra com 60 elementos o Percentil_25 = 25 * 50 / 100 = 15
Isso significa que 25% dos elementos estão abaixo da posição 15, ou seja, do valor que a variável representa.
Se estivéssemos observando uma variável que representa a velocidade e nessa posição o valor fosse 30 km/h, 25% dos valores estão abaixo dos 30 km/h ou 75% acima. O percentil 50 é o que divide a amostra ao meio.
Quando a medida é o quartil, a referência é a divisão do espaço em quatro partes, ou seja, os percentis 25, 50 e 75 são o primeiro, segundo e terceiro quartil. O segundo quartil equivale ao percentil 50 que representa a mediana da amostra.
A figura 1 mostra a denominação das partes do boxplot.
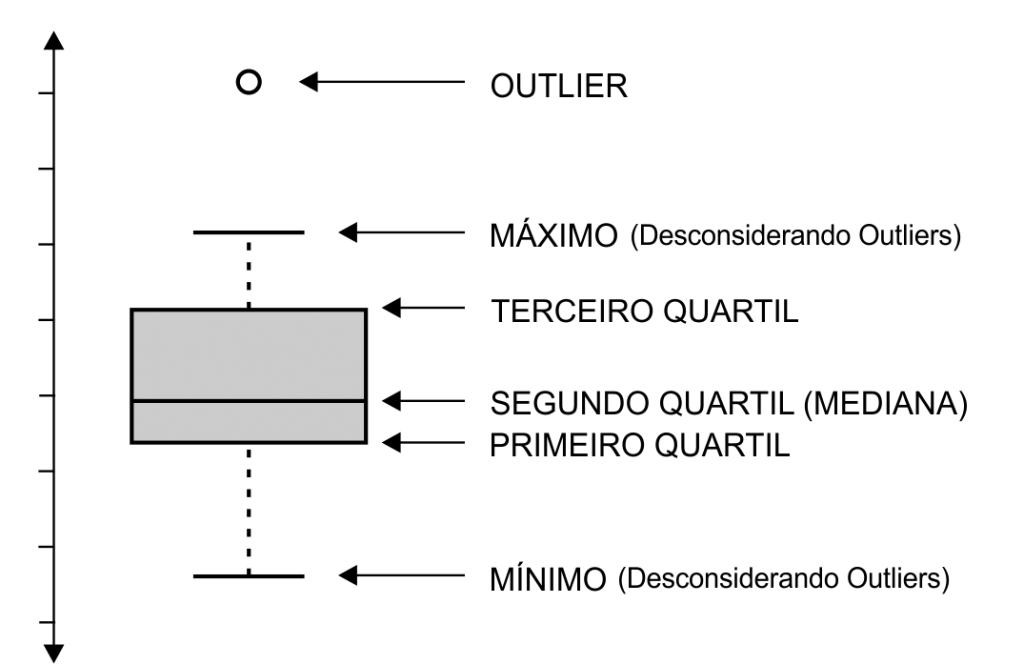
Interpretação do boxplot
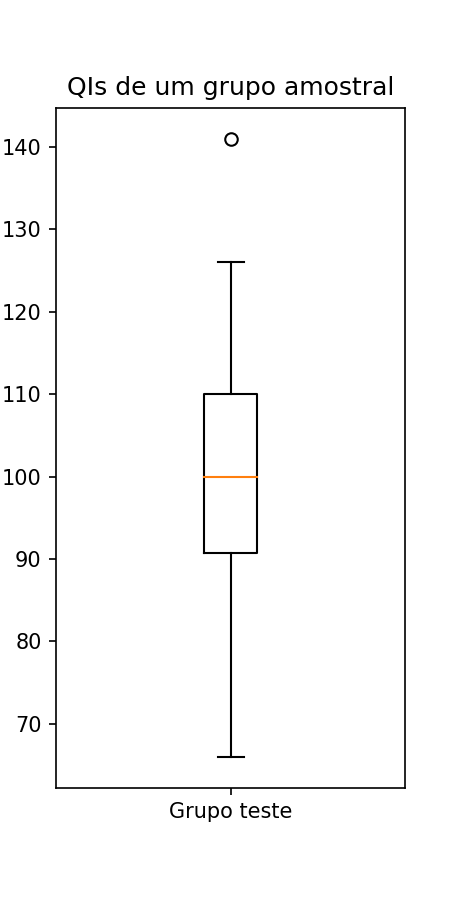
O boxplot é observado em sua totalidade e também em partes. A Figura 2 mostra um boxplot para uma amostra que representa os QIs de 100 pessoas. Observa-se que existe um valor considerado outlier, ou seja, anômalo quando este encontra-se fora do eixo do boxplot. Os outliers são determinados pela distância interquartílica, que é dada pela diferença entre o primeiro e terceiro quartil, ou seja, entre 25% e 75% da amostra. Compara-se as caudas para ver o tamanho das distribuições, a cauda inferior demostra que a sua distribuição é maior do que a cauda superior. Os dados não apresentam simetria, pois a mediana não encontra-se no centro do box. Os dados são considerados assimétricos positivos, pois os dados estão mais próximos do primeiro quartil.
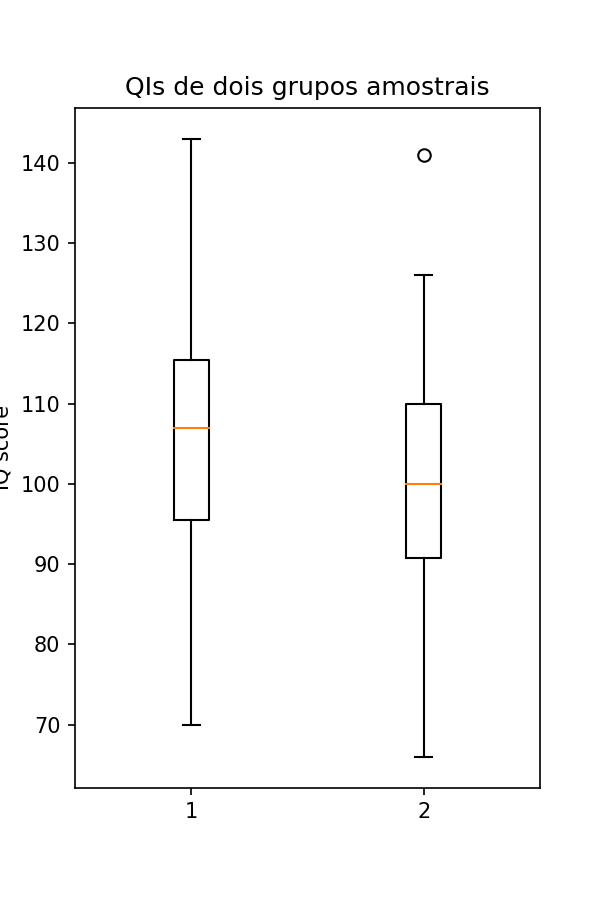
No segundo exemplo, analisamos dois boxplots que representam dois grupos de dados referentes a amostras de QI. Na comparação o grupo 1 apresenta uma mediana maior que a do grupo 2, além de não possuir outlier e a distribuição de dados abaixo dos 25% e acima dos 75% serem maiores que o grupo 2. O grupo 1 também apresenta assimetria e está é negativa, pois está mais próxima do terceiro quadrante. A variabilidade do QI do grupo 1, é um pouco maior que a do grupo 2.
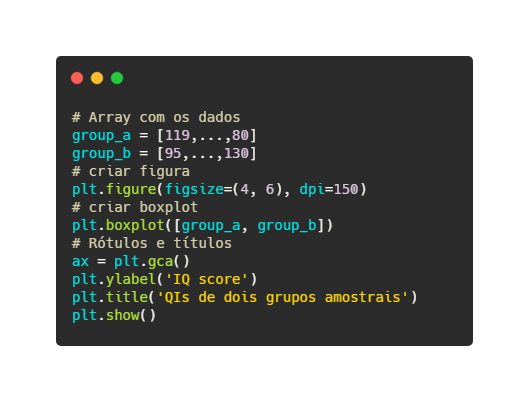
A Figura 4 mostra o código para gerar o último boxplot.
Conclusão
Com a utilização do boxplot pode-se resumir e representar graficamente a distribuição de uma ou mais variáveis, obtendo-se rapidamente medidas como mediana, quartis e a visualização de outliers.
Bom, esta é uma abordagem bem resumida sobre a utilização do boxplot e como fazê-lo em Python. Em breve, colocarei um post com uma abordagem mais avançada, mostrando como personalizar cada elemento do boxplot. Em caso de dúvidas ou querendo mais detalhes é só entrar em contato.
